第一章 单元测试
1、判断题:
设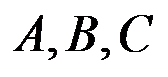 是欧氏平面上三个点,连接这三个点的最小Steiner树长度必小于这三个点形成的赋权完全图的最小生成树长度。( )
是欧氏平面上三个点,连接这三个点的最小Steiner树长度必小于这三个点形成的赋权完全图的最小生成树长度。( )
选项:
A:错
B:对
答案: 【错】
2、单选题:
以下对背包问题最优解的描述,正确的是( )
选项:
A:对于离散形式的背包问题,最优解中放入背包的物品大小之和为背包的容量。
B:对于连续形式的背包问题,最优解中放入背包的物品大小之和为背包的容量。
C:对于连续形式的背包问题,放入背包的物品大小之和为背包容量的解必为最优解。
D:对于离散形式的背包问题,放入背包的物品大小之和为背包容量的解必为最优解。
答案: 【对于连续形式的背包问题,最优解中放入背包的物品大小之和为背包的容量。
】
3、单选题:
考虑下面的批排序问题。若干个工件需在一台批处理机上加工,工件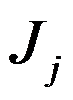 的大小为
的大小为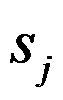 。大小之和不超过
。大小之和不超过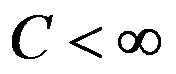 的若干个工件可作为一批同时加工,每批的加工时间均相等。工件的完工时间定义为它所在批的完工时间,目标为极小化工件最大完工时间。与该问题等价的问题是( )。
的若干个工件可作为一批同时加工,每批的加工时间均相等。工件的完工时间定义为它所在批的完工时间,目标为极小化工件最大完工时间。与该问题等价的问题是( )。
选项:
A: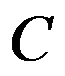 台机器的平行机排序问题
台机器的平行机排序问题
B:背包容量为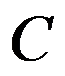 的背包问题
的背包问题
C:其他选项都不对
D:箱容量为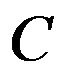 的一维装箱问题
的一维装箱问题
答案: 【箱容量为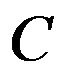 的一维装箱问题
的一维装箱问题
】
4、多选题:
以下字符集,不能作为字母表的是( )。
选项:
A: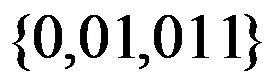
B: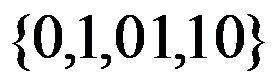
C: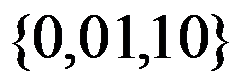
D: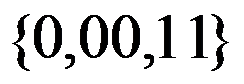
答案: 【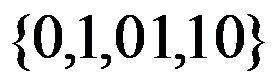
;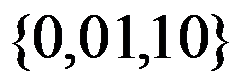
;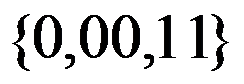
】
5、多选题:
考虑单台机排序问题,工件集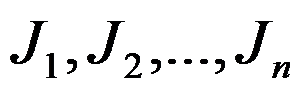 依次在一机器上加工,机器在同一时间只能加工一个工件,工件
依次在一机器上加工,机器在同一时间只能加工一个工件,工件 的加工时间为
的加工时间为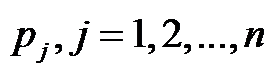 ,则所有工件的完工时间之和为( )。
,则所有工件的完工时间之和为( )。
选项:
A: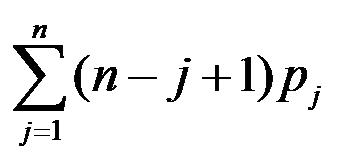
B: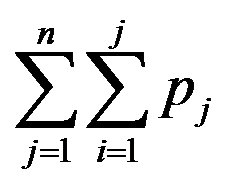
C: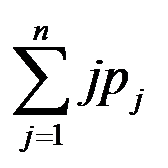
D: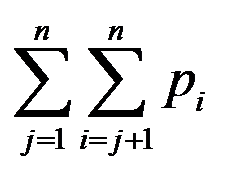
答案: 【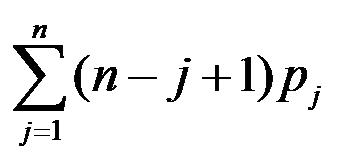
;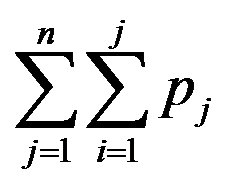
】
第二章 单元测试
1、判断题:
若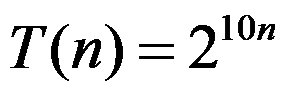 ,则
,则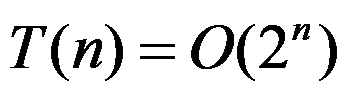 。 ( )
。 ( )
选项:
A:对
B:错
答案: 【错】
2、单选题:
设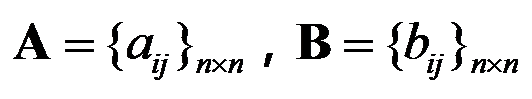 为
为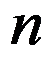 阶方阵。现用以下算法求
阶方阵。现用以下算法求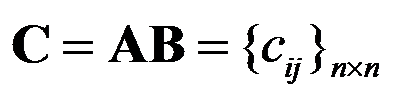 。
。
算法:
For i = 1 to n do
For j = 1 to n do
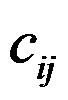 = 0
= 0
For k = 1 to n do
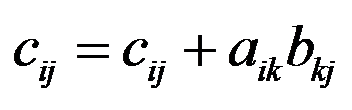
输出
该算法的时间复杂度为( )。
选项:
A: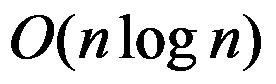
B: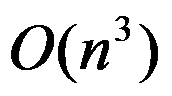
C: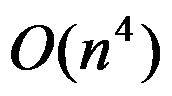
D: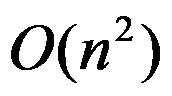
答案: 【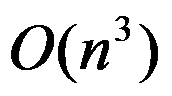
】
3、单选题:
若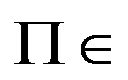 NP,以下能说明
NP,以下能说明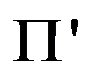 是NP-C问题的是( )。
是NP-C问题的是( )。
选项:
A:对任意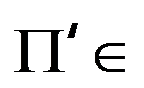 NP,
NP,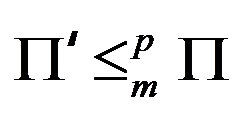 。
。
B:存在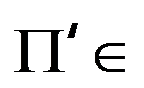 NP,
NP,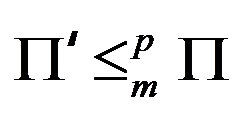 。
。
C:对任意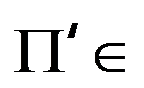 NP-C,
NP-C,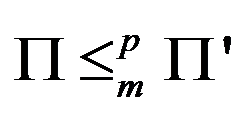 。
。
D:存在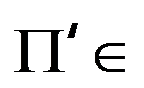 NP-C,
NP-C,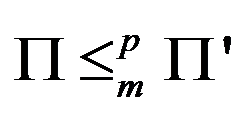 。
。
答案: 【对任意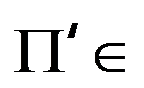 NP,
NP,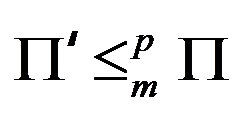 。
。
】
4、多选题:
设有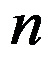 个城市的TSP问题实例,城市之间距离为
个城市的TSP问题实例,城市之间距离为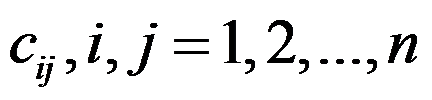 ,以下是该实例规模合理表达式的有( )。
,以下是该实例规模合理表达式的有( )。
选项:
A: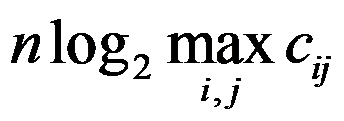
B: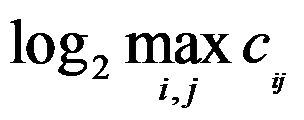
C: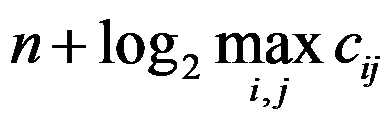
D: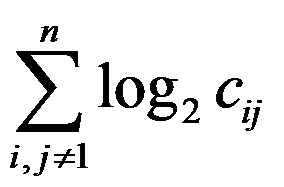
答案: 【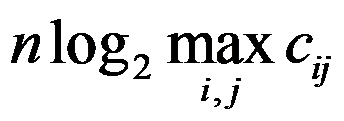
;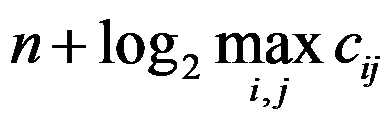
;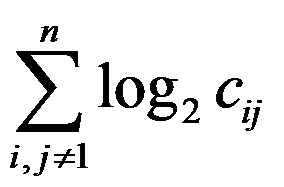
】
5、多选题:
设一平行机排序问题算法的时间复杂度为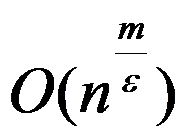 ,其中
,其中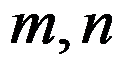 分别为机器数和工件数,
分别为机器数和工件数,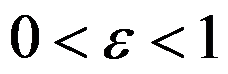 为一与实例无关的常数。以下说法准确的有( )。
为一与实例无关的常数。以下说法准确的有( )。
选项:
A:若在该问题中,机器数可能随实例不同而变化,该算法是一个指数时间算法。
B:若在该问题中,机器数是一个固定常数,该算法是一个指数时间算法。
C:若在该问题中,机器数可能随实例不同而变化,该算法是一个多项式时间算法。
D:若在该问题中,机器数是一个固定常数,该算法是一个多项式时间算法。
答案: 【若在该问题中,机器数可能随实例不同而变化,该算法是一个指数时间算法。
;若在该问题中,机器数是一个固定常数,该算法是一个多项式时间算法。
】
第三章 单元测试
1、判断题:
设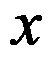 是取值在
是取值在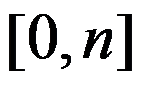 中的整变量,
中的整变量,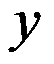 为0-1变量,“
为0-1变量,“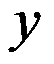 取值为1当且仅当
取值为1当且仅当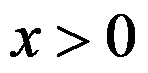 ”可用
”可用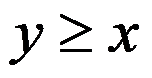 来表示。( )
来表示。( )
选项:
A:对
B:错
答案:
2、单选题:
考虑背包问题的下述算法,首先将物品按某种顺序排列,随后逐个放入背包,直至有物品不能放入背包时,算法终止。以下物品排列顺序,可使该算法的最坏情况比为有限常数的是( )。
选项:
A:其他选项都不是。
B:将物品按价值密度从大到小的顺序排列。
C:将物品按价值从大到小的顺序排列。
D:将物品按大小从大到小的顺序排列。
答案:
3、单选题:
某员工的购物车内有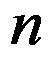 件商品,其中商品
件商品,其中商品 的价格为
的价格为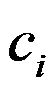 。定义
。定义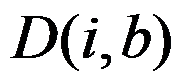 为员工使用不超过
为员工使用不超过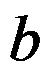 的资金,仅考虑购买购物车中前
的资金,仅考虑购买购物车中前 件商品时所能购买的商品价格之和的最大值,则
件商品时所能购买的商品价格之和的最大值,则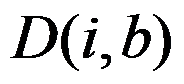 满足的递推关系为( )
满足的递推关系为( )
选项:
A: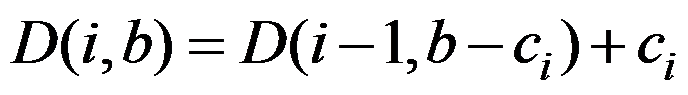 。
。
B: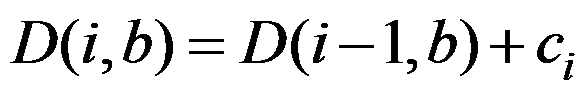 。
。
C: 。
。
D: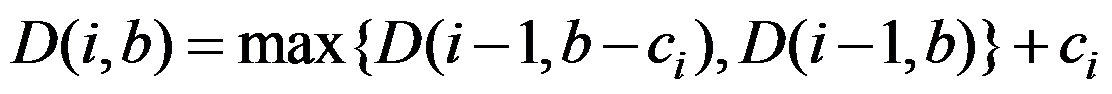 。
。
答案:
4、多选题:
考虑下面的排序问题,现有两台机器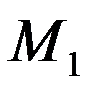 和
和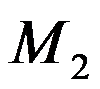 以及
以及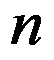 个工件
个工件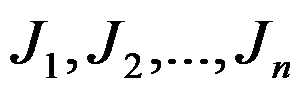 。每个工件需先在
。每个工件需先在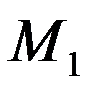 上加工再在
上加工再在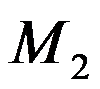 上加工后才能完工。工件
上加工后才能完工。工件 在
在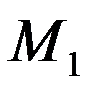 和
和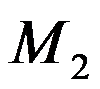 上加工所需的时间分别为
上加工所需的时间分别为 和
和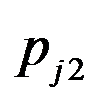 ,
,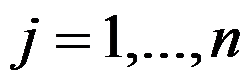 。一台机器在同一时刻只能加工一个工件。目标为最大工件完工时间尽可能小。该问题最优值的下界有( )。
。一台机器在同一时刻只能加工一个工件。目标为最大工件完工时间尽可能小。该问题最优值的下界有( )。
选项:
A: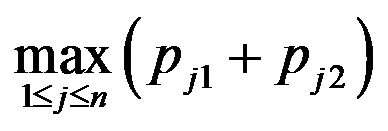
B: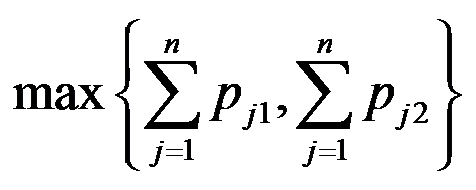
C: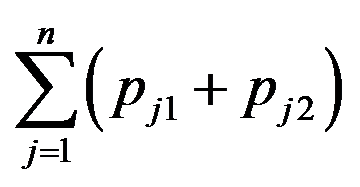
D: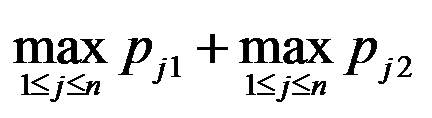
答案:
5、多选题:
设算法A为一极小化目标优化问题的近似算法,现用比较算法A给出的实例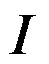 的可行解目标值
的可行解目标值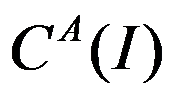 和
和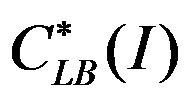 的方法证明算法A的最坏情况比,其中
的方法证明算法A的最坏情况比,其中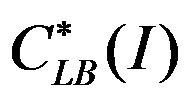 是实例
是实例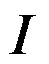 的最优值的下界,满足
的最优值的下界,满足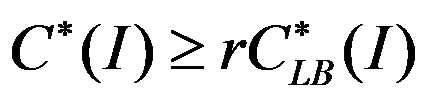 对任意实例
对任意实例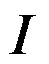 成立。以下说法正确的有( )。
成立。以下说法正确的有( )。
选项:
A:算法A的最坏情况比可能小于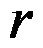 。
。
B:可能存在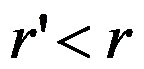 ,使得对任意实例
,使得对任意实例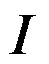 ,
,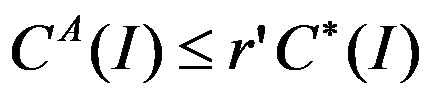 。
。
C:可能存在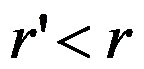 ,使得对任意实例
,使得对任意实例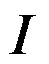 ,
,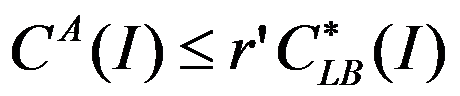 。
。
D:用上述方法,不可能证得算法A的最坏情况比小于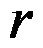 。
。
答案:
第四章 单元测试
1、判断题:
若博弈的某个策略组合不是Nash均衡,则每位参与者均可通过单方面改变自身的策略使其费用减少。( )
选项:
A:对
B:错
答案:
2、单选题:
考虑背包问题的在线形式。背包容量事先已知,物品一个个相继出现,物品出现后方知其价值和大小。具体地,第 个物品在第
个物品在第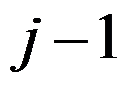 个物品是否放入背包已被确定后才出现,且此前已作出的前
个物品是否放入背包已被确定后才出现,且此前已作出的前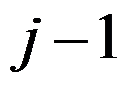 个物品是否被放入背包的决定不可更改。该在线问题的下界为( )。
个物品是否被放入背包的决定不可更改。该在线问题的下界为( )。
选项:
A:4
B:2
C:
D:3
答案:
3、多选题:
设一博弈的社会费用为极小化目标,记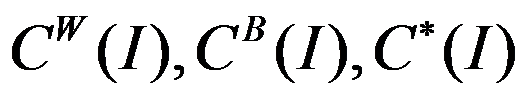 分别为实例
分别为实例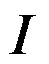 的社会费用最大的Nash均衡的社会费用,社会费用最小的Nash均衡的社会费用和最优社会费用。以下说法准确的有( )。
的社会费用最大的Nash均衡的社会费用,社会费用最小的Nash均衡的社会费用和最优社会费用。以下说法准确的有( )。
选项:
A: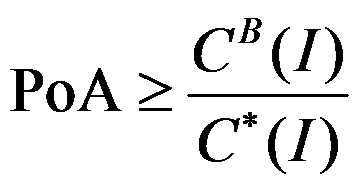
B: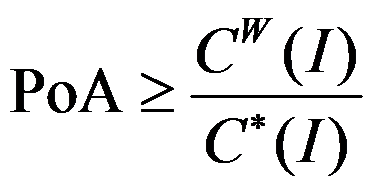 。
。
C: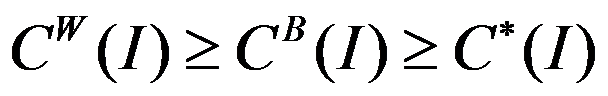 。
。
D: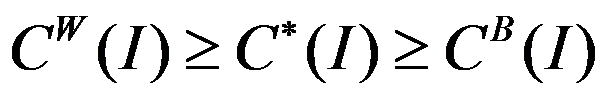 。
。
答案:
4、多选题:
设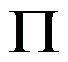 是一个在线问题,以下说法准确的有( )。
是一个在线问题,以下说法准确的有( )。
选项:
A:若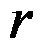 是
是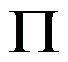 的一个下界,则可能存在竞争比小于
的一个下界,则可能存在竞争比小于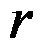 的在线算法。
的在线算法。
B:若存在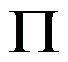 的竞争比为
的竞争比为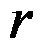 的在线算法,则问题的下界至少为
的在线算法,则问题的下界至少为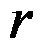 。
。
C:若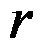 是
是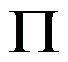 的一个下界,则可能存在竞争比大于
的一个下界,则可能存在竞争比大于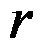 的在线算法。
的在线算法。
D:若存在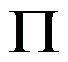 的竞争比为
的竞争比为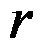 的在线算法,则问题的下界至多为
的在线算法,则问题的下界至多为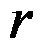 。
。
答案:
5、多选题:
一寝室住有四名同学。一日学园举行某项活动,有至少两名同学参与该项活动的寝室将获得奖励。每位同学有参加或不参加两种选择。他们都希望寝室能获得奖励,同时倾向于自己不参加活动。当然在自己参加活动而寝室获得奖励与自己不参加活动而寝室未获奖励之间更偏好前种情况。该博弈的Nash均衡有( )。
选项:
A:任一名同学参加活动或任一名同学不参加活动。
B:四名同学参加活动。
C:四名同学均不参加活动。
D:两名同学参加活动。
答案:


请先 !