绪论 单元测试
1、多选题:
数学分析利用极限主要研究函数的
选项:
A:可积性
B:连续性
C:可微性
D:周期性
答案: 【可积性;连续性;可微性】
2、单选题:
数学分析研究函数的主要工具是
选项:
A:函数的极限
B:函数的积分
C:函数的初等性质
D:函数的导数
答案: 【函数的极限】
3、单选题:
数学分析的研究对象是
选项:
A:可导函数
B:连续函数
C:极限
D:函数
答案: 【函数】
第一章 单元测试
1、判断题:
单调数列收敛的充分必要条件是它有收敛子列。( )
选项:
A:对
B:错
答案: 【对】
2、判断题:
无界数列一定是无穷大数列。( )
选项:
A:错
B:对
答案: 【错】
3、判断题:
数列有界是数列收敛的充分条件。( )
选项:
A:对
B:错
答案: 【错】
4、单选题:
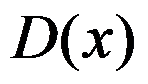 的周期为( )。
的周期为( )。
选项:
A:R
B:正有理数
C:无周期
D:正无理数
答案: 【正有理数】
5、单选题:
若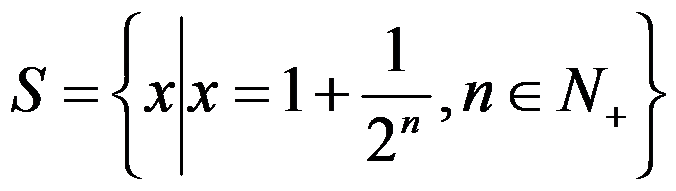 ,则
,则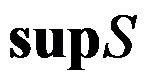 =( )
=( )
选项:
A:
B: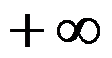
C:
D: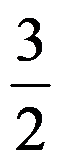
答案: 【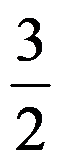 】
】
6、单选题:
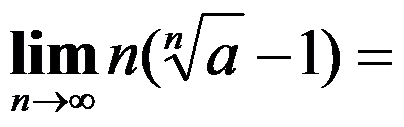 ( )。
( )。
选项:
A:
B:
C: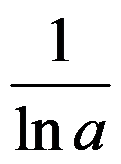
D: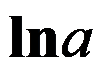
答案: 【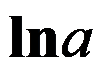 】
】
7、单选题:
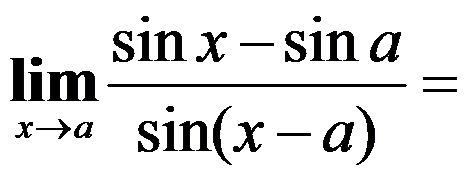 ( )。
( )。
选项:
A:
B:
C: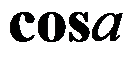
D:
答案: 【 】
】
8、单选题:
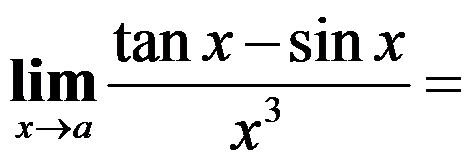 ( )。
( )。
选项:
A: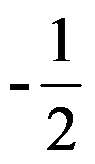
B: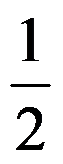
C:
D:0
答案: 【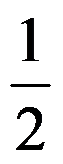 】
】
9、单选题:
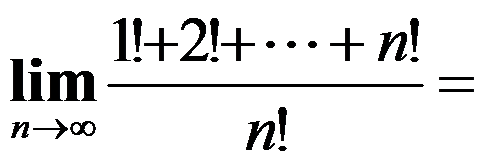 ( )。
( )。
选项:
A: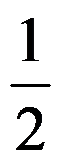
B:1
C:0
D:
答案: 【1】
10、单选题:
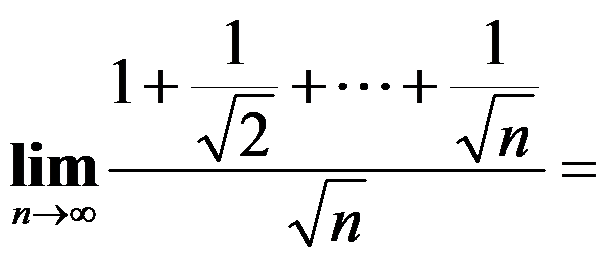 ( )。
( )。
选项:
A:2
B:
C:1
D: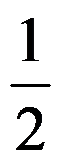
答案: 【2】
第二章 单元测试
1、判断题:
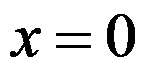 为
为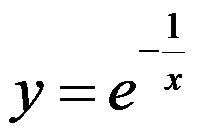 的第二类间断点。( )
的第二类间断点。( )
选项:
A:错
B:对
答案: 【对】
2、判断题:
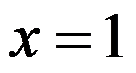 为
为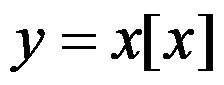 的跳跃间断点。( )
的跳跃间断点。( )
选项:
A:错
B:对
答案: 【对】
3、判断题:
若使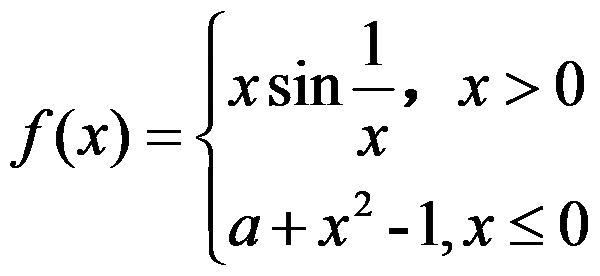 在
在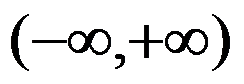 内连续,
内连续,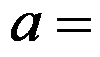 1。( )
1。( )
选项:
A:错
B:对
答案: 【对】
4、判断题:
不连续函数的平方仍为不连续函数。( )
选项:
A:对
B:错
答案: 【错】
5、判断题:
设f在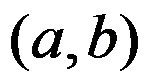 与
与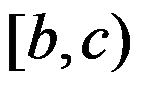 上均一致连续,则f 在
上均一致连续,则f 在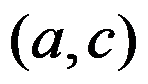 上一致连续。( )
上一致连续。( )
选项:
A:对
B:错
答案: 【错】
6、判断题:
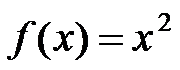 在
在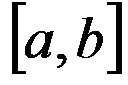 上一致连续.. ( )
上一致连续.. ( )
选项:
A:对
B:错
答案: 【对】
7、判断题:
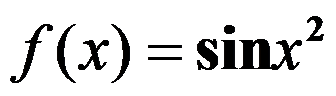 在
在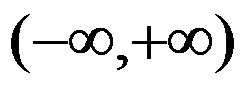 上一致连续.. ( )
上一致连续.. ( )
选项:
A:对
B:错
答案: 【错】
8、判断题:
设f为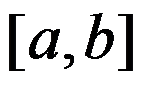 上的增函数,其域值
上的增函数,其域值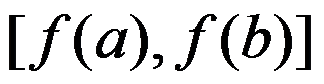 . 证明f在
. 证明f在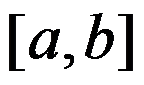 上连续. ( )
上连续. ( )
选项:
A:错
B:对
答案: 【对】
9、单选题:
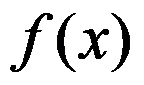 在
在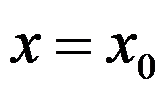 处有定义是
处有定义是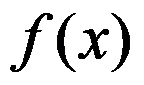 在
在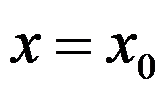 处连续的( )条件。
处连续的( )条件。
选项:
A:无关
B:充分
C:充要
D:必要
答案: 【必要】
10、单选题:
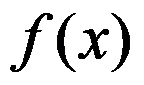 在
在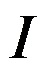 连续是
连续是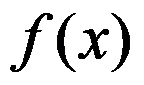 在
在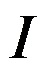 处一致连续的( )条件。
处一致连续的( )条件。
选项:
A:无关
B:充要
C:充分
D:必要
答案: 【必要】
第三章 单元测试
1、判断题:
函数在一点处可导是函数在这一点连续的充分条件。( )
选项:
A:对
B:错
答案:
2、判断题:
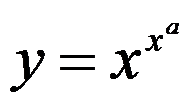 ,则
,则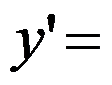
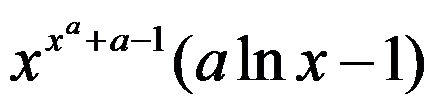 。( )
。( )
选项:
A:对
B:错
答案:
3、判断题:
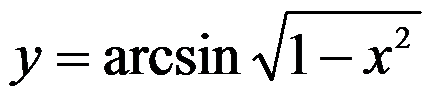 ,则
,则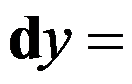
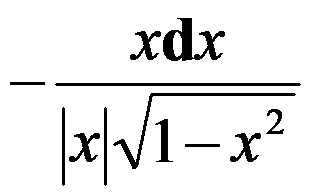 。( )
。( )
选项:
A:对
B:错
答案:
4、判断题:
函数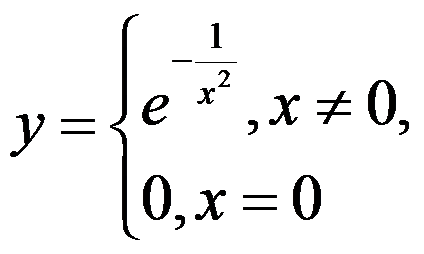 在
在 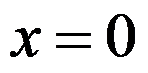 处有
处有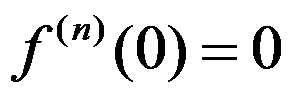 。 ( )
。 ( )
选项:
A:对
B:错
答案:
5、判断题:
Riemann函数在【0,1】上的任意点处可微。( )
选项:
A:错
B:对
答案:
6、判断题:
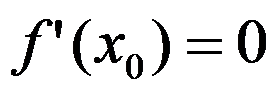 是函数
是函数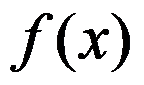 在
在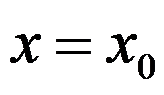 处取得极值的充分条件。( )
处取得极值的充分条件。( )
选项:
A:错
B:对
答案:
7、判断题:
导函数不存在第一类不连续点。( )
选项:
A:错
B:对
答案:
8、单选题:
设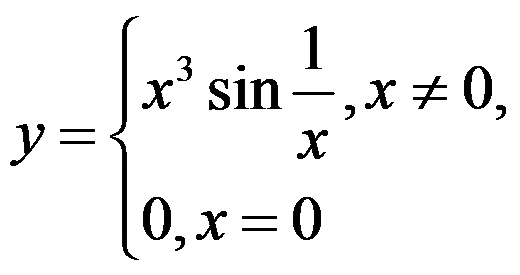 在
在 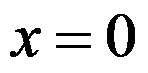 处( )。
处( )。
选项:
A:不连续但可导
B:不连续且不可导
C:连续且不可导
D:连续且可导
答案:
9、单选题:
设曲线方程x = 1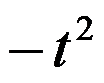 ,y =
,y = 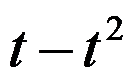 ,求它在点t=1处的切线方程为( )
,求它在点t=1处的切线方程为( )
选项:
A:
B:
C:y=-2x
D:
答案:
10、单选题:

选项:
A:1
B:-1
C:2
D:0
答案:
第四章 单元测试
1、单选题:
函数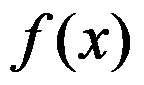 在
在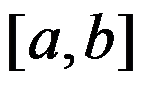 上可积的必要条件是( )
上可积的必要条件是( )
选项:
A:单调
B:连续
C:有界
D:存在原函数
答案:
2、单选题:
设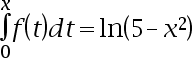 ,则
,则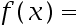 ( )。
( )。
选项:
A: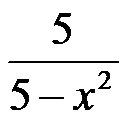
B: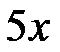
C: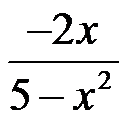
D: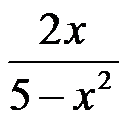
答案:
3、单选题:
已知反常积分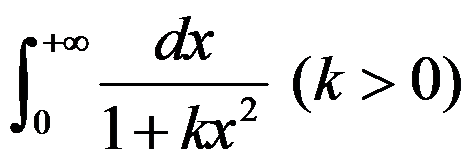 收敛于1,则
收敛于1,则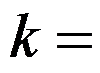 ( )
( )
选项:
A: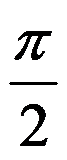
B: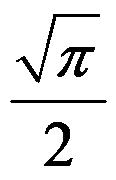
C: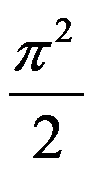
D: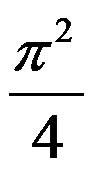
答案:
4、单选题:
下列反常积分收敛的是( )。
选项:
A:
B: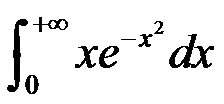
C: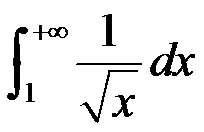
D: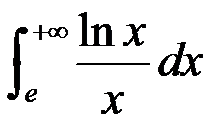
答案:
5、判断题:
若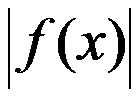 在
在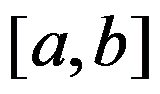 上可积,则
上可积,则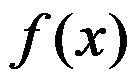 在
在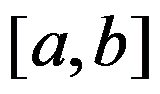 上可积;( )
上可积;( )
选项:
A:对
B:错
答案:
6、判断题:
若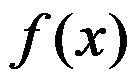 是区间
是区间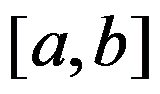 上的只有有限个间断点的函数,则
上的只有有限个间断点的函数,则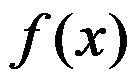 在
在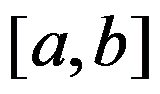 上可积;( )
上可积;( )
选项:
A:错
B:对
答案:
7、判断题:
瑕积分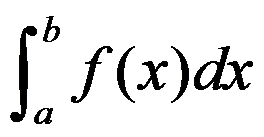 收敛时,
收敛时,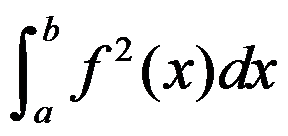 一定收敛;( )
一定收敛;( )
选项:
A:错
B:对
答案:
8、判断题:
若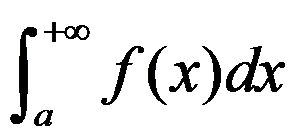 收敛,且
收敛,且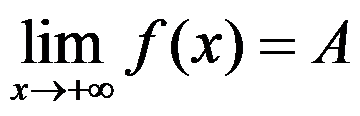 ,则
,则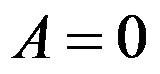 ;( )
;( )
选项:
A:对
B:错
答案:
9、判断题:
若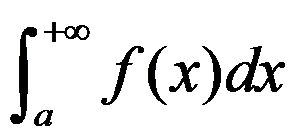 收敛,则
收敛,则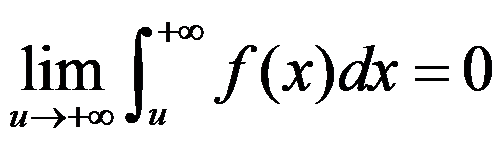 ;( )
;( )
选项:
A:对
B:错
答案:
10、判断题:
积分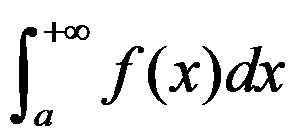 收敛时,
收敛时,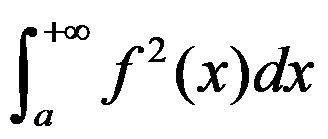 一定收敛;( )
一定收敛;( )
选项:
A:错
B:对
答案:
第五章 单元测试
1、单选题:
1.下列级数中条件收敛的是( )
选项:
A: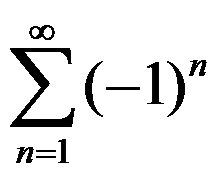
B: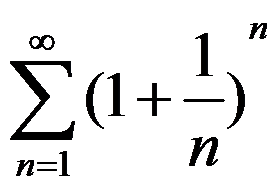
C: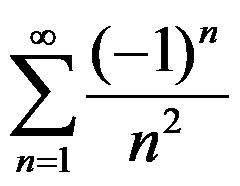
D: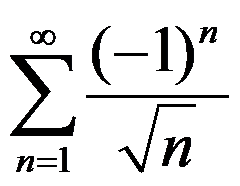
答案:
2、单选题:
2.若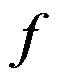 是
是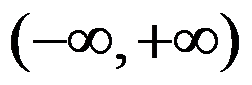 内以
内以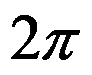 为周期的按段光滑的函数, 则
为周期的按段光滑的函数, 则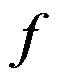 的傅里叶(Fourier)级数在它的间断点
的傅里叶(Fourier)级数在它的间断点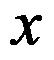 处 ( )。
处 ( )。
选项:
A:收敛于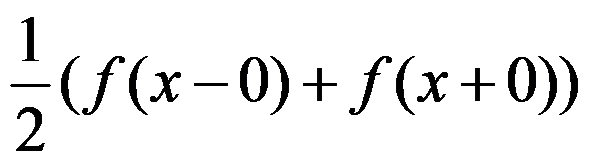
B:可能收敛也可能发散
C:发散
D:收敛于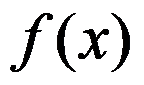
答案:
3、单选题:
3. 收敛,则( )
收敛,则( )
选项:
A: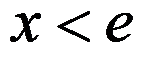
B: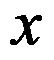 为任意实数
为任意实数
C: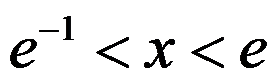
D: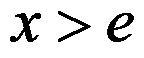
答案:
4、单选题:
4.级数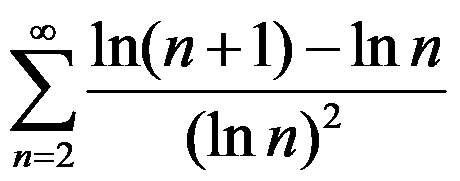 为( )级数。
为( )级数。
选项:
A:绝对收敛
B:收敛
C:发散
D:条件收敛
答案:
5、单选题:
5.幂级数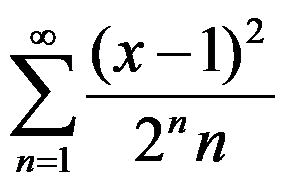 的收敛域为( )。
的收敛域为( )。
选项:
A: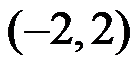
B: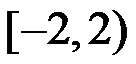
C: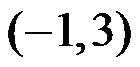
D: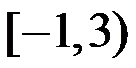
答案:
6、判断题:
6.若级数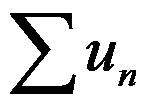 与
与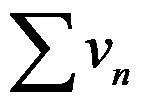 均发散,则级数
均发散,则级数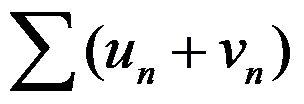 必发散。( )
必发散。( )
选项:
A:对
B:错
答案:
7、判断题:
7.若级数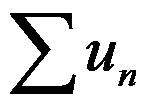 对每个固定的
对每个固定的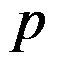 满足条件
满足条件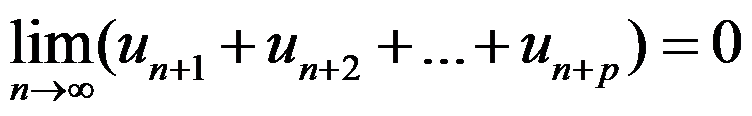 ,则此级数必收敛。( )
,则此级数必收敛。( )
选项:
A:错
B:对
答案:
8、判断题:
8.若级数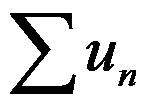 收敛,则级数
收敛,则级数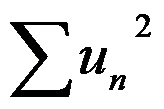 必收敛。( )
必收敛。( )
选项:
A:对
B:错
答案:
9、判断题:
9.若级数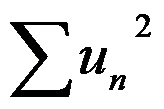 收敛,则级数
收敛,则级数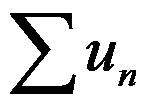 必收敛。( )
必收敛。( )
选项:
A:对
B:错
答案:
10、判断题:
第六章 单元测试
1、判断题:
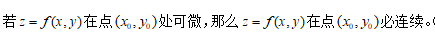
选项:
A:错
B:对
答案:
2、判断题:

选项:
A:错
B:对
答案:
3、判断题:

选项:
A:错
B:对
答案:
4、判断题:

选项:
A:错
B:对
答案:
5、单选题:
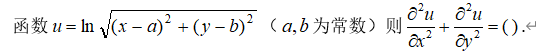
选项:
A:-1
B:0
C:1
D:无法计算
答案:
6、单选题:
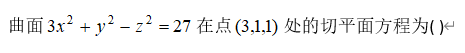
选项:
A: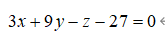
B: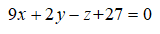
C:![]()
答案:
7、单选题:
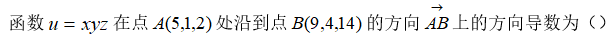
选项:
A: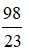
B: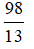
C:
D: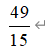
答案:
8、单选题:
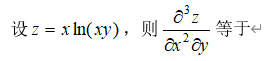
选项:
A:0
B: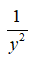
C: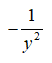
D: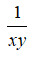
答案:
9、单选题:
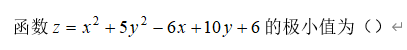
选项:
A:-6
B:0
C:不存在
D:-8
答案:
10、单选题:
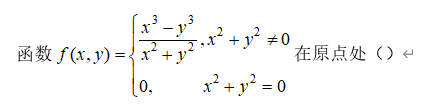
选项:
A:
B:
C:其余答案均不正确
D:不可微
答案:
第七章 单元测试
1、判断题:
若函数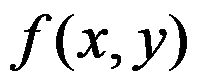 在有界区域D上有界,则函数
在有界区域D上有界,则函数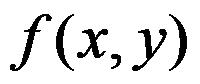 在
在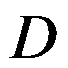 上可积。 ( )
上可积。 ( )
选项:
A:错
B:对
答案:
2、判断题:
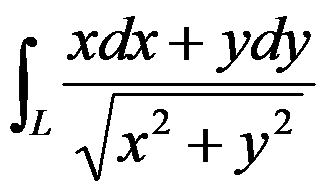 与路径无关,其中
与路径无关,其中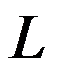 沿不通过原点的路线。( )
沿不通过原点的路线。( )
选项:
A:对
B:错
答案:
3、判断题:
改变积分次序,
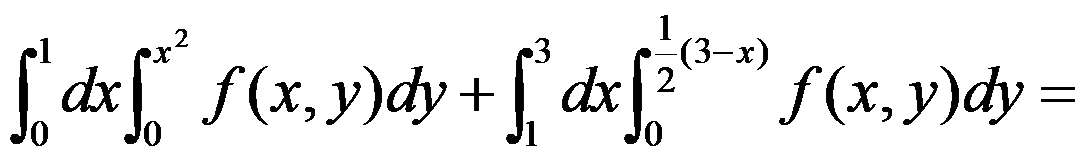
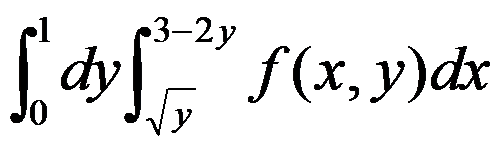 。( )
。( )
选项:
A:对
B:错
答案:
4、判断题:
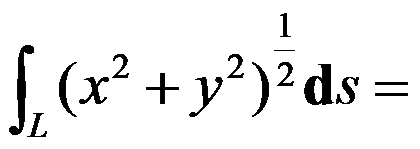
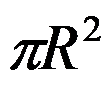 ,其中
,其中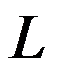 是以原点为圆心,
是以原点为圆心, 为半径的右半圆周。( )
为半径的右半圆周。( )
选项:
A:错
B:对
答案:
5、单选题:
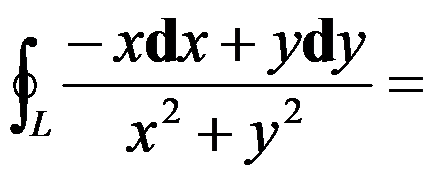 ( ),其中
( ),其中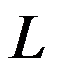 为圆周
为圆周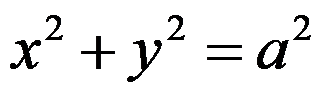 ,依逆时针方向.
,依逆时针方向.
选项:
A: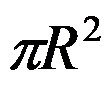
B: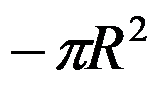
C:0
D: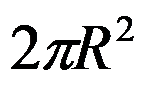
答案:
6、单选题:
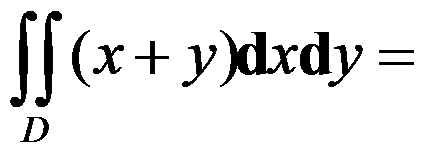 ( ),其中
( ),其中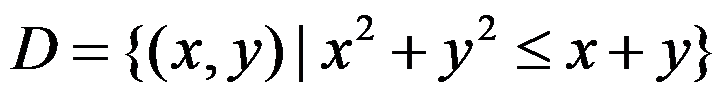 .
.
选项:
A:0
B:
C: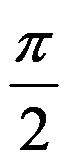
D: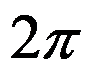
答案:
7、单选题:
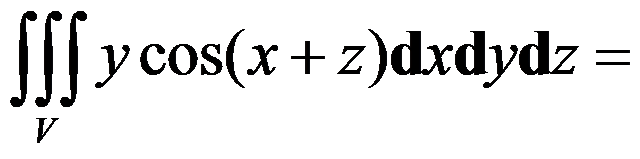 ( ),其中
( ),其中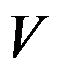 是由
是由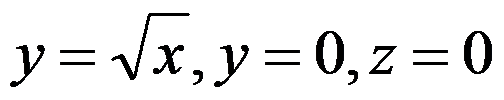 及
及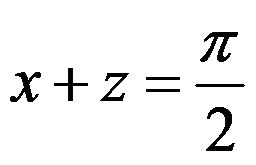 所围成的区域.
所围成的区域.
选项:
A: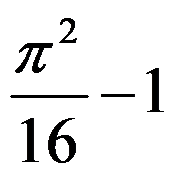
B: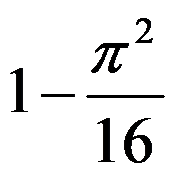
C: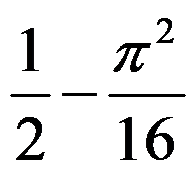
D: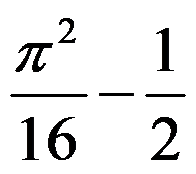
答案:
8、单选题:
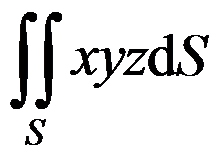 =( ),其中
=( ),其中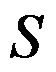 为平面
为平面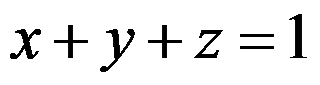 在第一卦限的部分.
在第一卦限的部分.
选项:
A: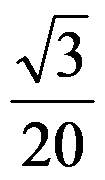
B: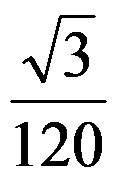
C: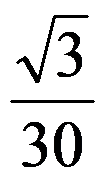
D: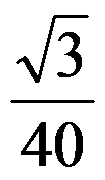
答案:
9、判断题:
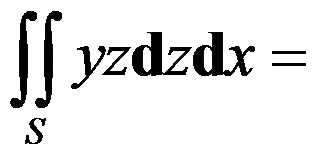
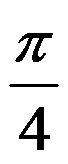 ,其中
,其中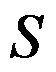 是球面
是球面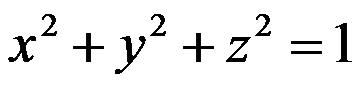 上半部分并取外侧为正向. ( )
上半部分并取外侧为正向. ( )
选项:
A:错
B:对
答案:
10、判断题:
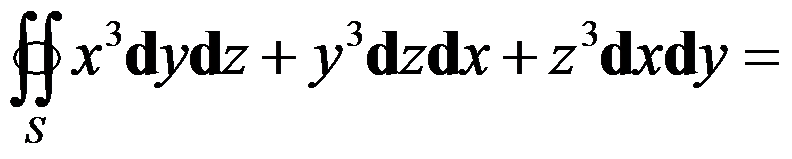
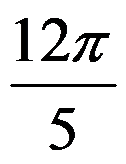 ,其中
,其中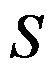 是单位球面
是单位球面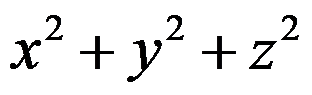
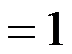 的外侧。( )
的外侧。( )
选项:
A:对
B:错
答案:
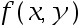 在
在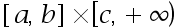 上非负连续,
上非负连续, 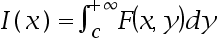 在
在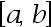 上连续,则
上连续,则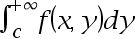 在
在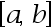 上一致收敛. ( )
上一致收敛. ( )

请先 !