绪论 单元测试
1、单选题:
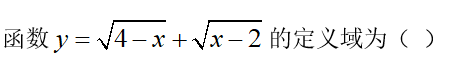
选项:
A: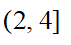
B: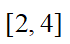
C: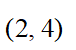
D: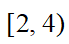
答案: 【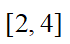 】
】
2、单选题:
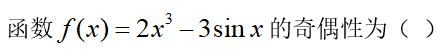
选项:
A:偶函数
B:非奇非偶函数
C:无法判断
D:奇函数
答案: 【奇函数 】
3、单选题:
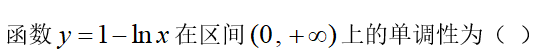
选项:
A: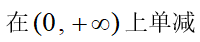
B: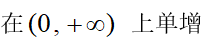
C: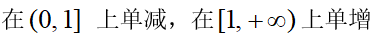
D: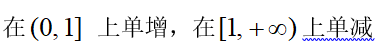
答案: 【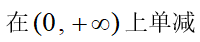 】
】
4、单选题:
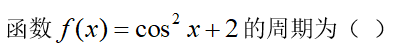
选项:
A: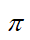
B: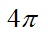
C: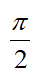
D: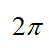
答案: 【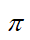 】
】
5、单选题:

选项:
A: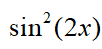
B: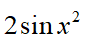
C: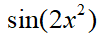
D: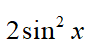
答案: 【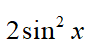 】
】
第一章 单元测试
1、单选题:
设函数是定义在
上的函数,则函数
在
上的奇偶性为
选项:
A:无法判断
B:奇函数
C:偶函数
D:非奇非偶函数
答案: 【奇函数】
2、单选题:
函数,当时
的极限为( )
选项:
A:不存在
B:0
C:2
答案: 【不存在】
3、单选题:
当时,
均为无穷小量,下列变量中,当
时,可能不是无穷小量的是( )
选项:
A:
B:
C:
D:
答案: 【】
4、单选题:
函数极限为
选项:
A:2
B:0
C:-1
D:
答案: 【2】
5、单选题:
函数极限为
选项:
A:
B:2
C:0
D:-1
答案: 【-1】
6、单选题:
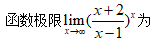
选项:
A: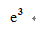
B: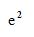
C:e
D:1
答案: 【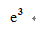 】
】
7、单选题:
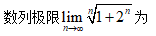
选项:
A:0
B:2
C:1
D:不存在
答案: 【2】
8、单选题:
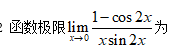
选项:
A:2
B:不存在
C:0
D:1
答案: 【1】
9、单选题:
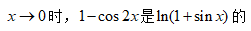
选项:
A:同阶无穷小,但不是等价无穷小
B:低阶无穷小
C:等价无穷小
D:高阶无穷小
答案: 【高阶无穷小
】
10、单选题:
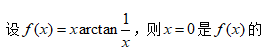
选项:
A:连续点
B:第二类间断点
C:可去间断点
D: 跳跃间断点
答案: 【可去间断点】
第二章 单元测试
1、单选题:

选项:
A:既非充分又非必要条件
B:充分条件
C:必要条件
D:充要条件
答案: 【必要条件】
2、单选题:
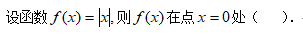
选项:
A:无法判断
B:连续,但不可导
C:连续且可导
D:可导不连续
答案: 【连续,但不可导
】
3、单选题:
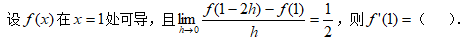
选项:
A: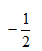
B:
C: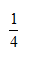
D: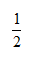
答案: 【 】
】
4、单选题:
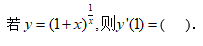
选项:
A: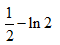
B:2
C:e
D: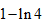
答案: 【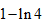 】
】
5、单选题:
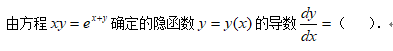
选项:
A: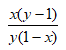
B:
C: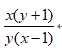
D: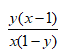
答案: 【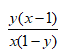 】
】
6、单选题:
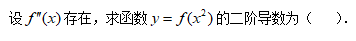
选项:
A: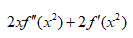
B: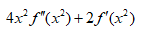
C: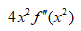
D:
答案: 【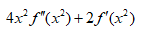 】
】
7、单选题:
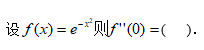
选项:
A:2
B:1
C:-1
D:-2
答案: 【-2】
8、单选题:
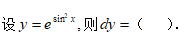
选项:
A: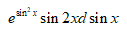
B: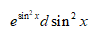
C: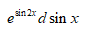
D: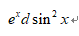
答案: 【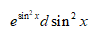 】
】
第三章 单元测试
1、单选题:

选项:
A:充分条件
B:充要条件
C:必要条件
D:既非充分也非必要条件
答案:
2、单选题:
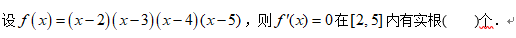
选项:
A:0
B:1
C:3
D:2
答案:
3、单选题:
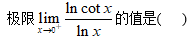
选项:
A:0
B:1
C: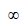
D:-1
答案:
4、单选题:
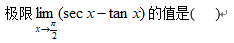
选项:
A:1
B: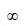
C: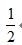
D:0
答案:
5、单选题:

选项:
A:1
B: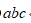
C: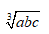
D:0
答案:
6、单选题:
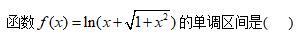
选项:
A: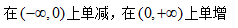
B: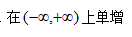
C: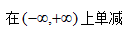
D:
答案:
7、单选题:
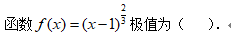
选项:
A:
B:
C:
D:
答案:
8、单选题:

选项:
A:下降,下凸
B:下降,上凸
C:上升,上凸
D:上升,下凸
答案:
9、单选题:
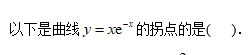
选项:
A: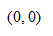
B: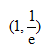
C: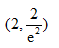
D: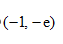
答案:
10、单选题:
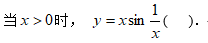
选项:
A:有且仅有水平渐近线
B:有且仅有铅直渐近线
C:既有水平渐近线,也有铅直渐近线
D:既无水平渐近线,也无铅直渐近线
答案:
11、单选题:
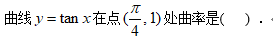
选项:
A:1
B:0
C: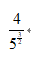
D: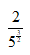
答案:
第四章 单元测试
1、单选题:
选项:
A:
B:
C:
D:
答案:
2、单选题:
选项:
A:
B:
C:
D:
答案:
3、单选题:
选项:
A:
B:
C:
D:
答案:
4、单选题:
选项:
A:
B:
C:
D:
答案:
5、单选题:
选项:
A:
<img src=”data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAALUAAAA1CAYAAAAH46pxAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAA7dSURBVHhe7ZsJXJTV+sd/MOybkCACmiCICG4ILpgLmlk3LUxzwdSbelPxpmWmYGTSTfOK5t+lrkvyV3AhVNwS01TcwVQQURBBZN8EhnVmmPW5Z+CtS2o2IIqN7/fzOR8+5znnZeZ5399Znue8o0MM8PBoEbrcXx4erYEXNY/WwYuaR+vgRc2jdfCi5tE6eFHzaB28qHm0Dl7UPFoHL2oerYMXNY/WwYuaR+vgRc2jdfCi5tE6eFHzaB28qHm0Dl7UPFoHL2oerYMXNY/W8cL/nEsll0AqU0IlMIaxkQC6KikkUhUgMICRgQA6XL+/CqSog1SqgFLXCEbGehCoZKiTMv90DWBs+Nfzpzm88DN1yblQrJg6Cu8t3I0T2VUovrgen30WipDodIi4Pn8lhFe2YMMHb2LinP8gOq0G5Ylh+PqLr7B4500IuT7azgsvasO2zujclt2IzAhExkRjRxzB0NIRrnam0OP6/JVoY9MJjrYmMMnfi0M/RWLLWTHkxk5wczCHPtdH29HS7YcUZanxSLp+F9kSztQYAwsYufTHG707wtqEjeuyWJzdvRYhCW7o5TsbQeO6wK4N1/c5QlKahttxcUgpVTEPH4T5Yd8bAwb0QXf9JCRF/QtB5+1g33cWPpvYCy7tuG6tSW0yTp5MRm55HRpEZwB9Yw8MGu8FZwMpaoVC5Ne0gUsHE+gJ6js0Cy0VdTVSdn+Fzd8dwc/lnKkxZp1g6ReIsABfdLdR372buBJ5CMsjXsLM1ZPg151N3c8hZclRiPzqS0QkK5mHD8L8GDAXiz+ejZmeRcg8EYmFa/XxTvAETBnSQd3aSiggrShETn4WhGcjERwVj5zSOu77mMLIfASmLB2LMd0yEBcvRYGZHxa8ZQNjg/oOzUJLRa2EpLwQ90sqUKXgTI1hQZPAyh6dbS3AYilGCuI37cHK9cDYH+ZhQu/2MKnv2FQIxGJMdTSmo9PyIZlCLER5YT7KxGoPH4GZHRzsbdDWKAu39+1GcHAFhn47F++PdEbzFp4W8Kf4JKI3/x8W7bwHXeUAjF85BaM92sG8vlEJee0NnPhqGw5kZELS2x9/X7gKHw/Qh8GT3D61qF90itOuUNhMf/potDcFn7hHGVKuoUlISSZOpIOLt9EPEVcpj7O2BpW5ybR7/hz65HUP+nT/VUqScA1NQsHKLToWEkY7N1ygzAZjk1DdiqD/zOpBrnYdSGd4EK39/2uUXcc1/kYu3VnzLrkbdSH7t9fRiRp2HdfSXAQhDE7fLxgyICcW4d/vws54XVg7W8FJcBh7YtJxV9EZLs4OsDHkumqEDHJJEqIXnkKOkS26vtkNz3Yby6bUoovYt30ntp4WwaijA9zNYnDweAqSKh3g7OoEO2Ouq0ao14IUHAk6gduVZugyoTccGho0gF1bcg7b14ZgRWQhRN7zEbpiIeaNcoTlQ9G3Odq666Eg1RTWL3thnJ8rrLiW5vLcZD8URSm4evIizmdWQZ0mbjCWoyjxMKKiohF14ibusgDjd5Qm4OJP+1h7FPZF/4gT52+jkAWGv17+eFiv2gLcvZmFSkML9H1vMrz7T4O77n2Iy8tQKee6aYwOW6INYGJpClNTtr3hrE1Gnou7lw9jL/Mpam80Dh6NR2qRSD0E/xxJMXJSM1EiN0KfSWPRd/As9DAUQ15WjPKHI0sN0IexhRlMzQybkAkiKETpSN22Fqt3JqHE8T3MDJ6LgL4NG46HYc/BkgW0Hs7oZW2BlzjrE8HN2K0EW2gk5VSUd44iP3mNeho4UqeAaEooZ4ufqITK4rbSxgBvcnbpSS6jvqHd18saLpNXUXnqZTq9egKN9HEhFxcXcupgTy49/GnpqQIqlGuygLE+CilJRCIS1cnrlzyVQsbqtSRmdY3+xe+QUF31cQrt/xGFBB6lVM6qOTISFeZQWuTntOAdD+Yz86tzR7K38qIJq3+meLF6O/AnKGVUJ2b+SGSkrK/LWZ35w+ryekNTkLFyjr4buYCWTI+kxAajBlRT6Y0NFNDegvQFL9Pw4B/p8mO3c3JWEigiPIYi99xpMD0hrTtTE5s+7uzHuiWBWBQWi2RZNgqOH8XJm0W4duzf2HI4Ful9vsGOiG3YtXI8RnSxZBdVIvvMd1g2NgDzDlqj34ffYteu3di4cCR6qi5g15E43C7UZF5jkYj61NDEBCaGevUnbToCfVY3hTGr6zU5UBFAINCtD6h0dHSbuAQqIas4hfA50zAxKBF5vT5D2K5dCN+0BDN6FODCqeOI+aWS6/sYdPVhaMz8MdJv+HxdPVZn/rC6XpOftHqtYX401R9JEYQJFxBTLYXc/W0MG+oNz8dmMtSf44ZRbw3GG39zbDA9Ia0rah22qNl6YrjfLCxZHYKQfwzCy1kx2PbZ+9hwxQRGPtPh7zcEg3z6on+PjmhnKsLdgxvxdfAPOGjig/GzZ+OD8a+jf/9++JtvL3SxqkJubjEqRJptQFoWJhz1gBAYwsjQlIvuNUGJ2qxj2D7/a4SmmMFx4izMe38Shvbvj4Ejh2GgqwDVpQXIK2nW/uEJUEvDDMZ6zB8DE439kZVkIfnSOQgFMnR+ZTj6uNvi8dk59exhgpeszGFp+QR5vEY8UUpPJS5F5rnt+CmhCiWPOuR4BCZuI+A7bChe6fDgeFKi7OxyzB0fgn0iR4xZvR9rA7zg1KhbTfpmbPxgBb5N8sbIA1ux7VWbhr2eIg2x//4cn4cVwypwJVa+64Oe1prvApuKSlKOrPPM72sVKBJzRiigkObiWmQm5J2c0G2YC6y5lnrae8PLdxjG9lCvNv9DURaP05sWY8kXZdAJ2YjvA0egj5G6RQLh+W+wYM4PSBo4C4s+mY4p7poPlaZAcjHy47bjeHwhsms4Y32gWICEyHTUmNvDbbQ72jc0NNDWA25DXsMUb5t6Wf5K+S9bsXHebKy7ZYuhq45i+Wxv9GgZrWrME4laWZmNq+H/xLrDJbj78GnAI7EcMgczZk7HZI+HQ6naO3sRHvgplmWMw/z1n+KLEY3j7UpcWz4KAaEFoKk7cPA7X3SUZ+P6L2nIu3IAB6Izcbfz3/HlhonwtTJsfqCmAarqPFyLYH4fKkT6b7sCFUhZi/sZVVCZW8DKoQ3qtfkrrmPgN30mlr5mxxnUKFDy87+wfH4oIo1DsOVYEMbZVaE4NQnXEq4g6dBRHCwZBP8vZ2HOq53YvPl0IGklUvZ8iA1705BYyhnrz/xEKM2ohEzfBFaOL/0+d//yqxgyLQBrxjg2Wu4JeWdDsXpGEMILfTDu+y0IntoDzlzrM0Mt6majVJC0tpyEZaVUWqpZKasSkVgdGzwCVWkcHf90CDlajaXZO5KohLPX50zFP9OmN1yojakPDV59mfLy71D+0aX07ggWVHXqT6NmRNAZkbIhQHraqBQkY35X/M7vPMrPiqJlXrNo8fw9dKmRz/VFWEM1dQ8Ee4pMurR6HPUT2JLlpG10LDmPCm5FUGjAIHJy6kZuPQNpc2IRVT5tp1RKkosqqLK88XcuZOUIrfKdQx/5b6XYxr6oi7CKqiQPBq8qKji3hhZ0AVkYetLU7cmUwbU8S56jw5cyqsg/QJtmvEM+BnY0OnA/xQq5Jqoh1dUVNNnLlqBrQeaO3cmzez/yHLWIvthxiM6cT6SU7Nr6DEbrcp7WD1xEK5eephzO8lgKj9C2AG8yhCEJ2jmTm0dP6jlwKk0L2U6Hz16iuIQi5nlrcpXC3gykZbMOkaZ5icpENiiHg9oYm9LwlZfoai3X8Axp3UCxERXX7yAjLh16IwfDx0uJe7evIz7t1w2rAXTKSlFQUwGj7q9g3NQZmDTZHxNZmT7RD76DPeHuoIu8yxdQKBajySnmFqEO0hoxpEoZpDKJZq+tioQovV8EqY0Dhr07B/5T/DHJfxKmTZ6Mt4cOhE+f9qhL/AXZ+bmt8Bqs+i6KUaeQQSbX0B+GmZ0jevdxgVgmQuKxOCRnPS7YYluc6jgcOXMHSVkt99RaT9QsyCxOOY2oq7koyErC/Xv3kFjXE/1eH4YBfc1RWZSFwuoS1JSkI257LG4ZWcHO2AACqQNc3lmAxUs+RuBkTziyjas49Sh2r1mDcBa41TzqXY/nFasOsG1jhjY1+jDsPgUfBQVhyYdv4tUuLLISpeFyeCjW/3gDaRpk854XBNau8BzFBqiPNaoubsWWVVtxJL7k4bcKa28jIXopVm2NRUKxhlkGDWm9Y3JhChL2BGNaWCoqs2/D2LkLdLzfgq+5LvTuHmA34j5ExiwYzcpD8plyWPj1QkdJGTJOXce1whpY2ihQnp2FrKx0XDm6G3E5ldAbOB2vuVrB7GlGiX+IAkppJi5sToWkkzN6vOH258fkJqYwkJah5FISYq/nQGEpgE55AfMpBzcvxuDCmXMocPHDwL690flpRYl/iDotmoNLW5MhNLWHx7hesG9oeDy6ZjCx74p+7aogrLiJqzEXcfZGFXSc9CDKUj+vhpJ++QiOnzyPs7W+mDhxEAY7NekM//Fw25BnjzCFroYOJ4/OttR+0AJa9lMOsTiPxRoiUpxfRu8Nc6J2Dl40YtJWOlZQRWL16V9JDG2bM5K62jhQJ2dncq4vg2jSknA6XlBKFXWqVtxXS6iu5hStGx5IK5cdpzTO+nhUpKhLoWthc2mEnQM5dHLifPKgV0YH0eYreZRbIyXpM4l+H0R9oniRvh+zhELm7qcbDUbNkVVR5b09tGYyC3qt7Kjjb8+rofiMn09rzhRSdpmoxf1rvVdPFWLUFt7B7ez7EOp1hmNXZ3Rtq94NsRlCVIw7GZnIK1bC2MYVPb3sueS/BFW5GUi9UwBhnaJ+LlEn7tt
B:
C:
D:
<img src=”data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAMQAAAA9CAYAAADyO8a6AAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAA7hSURBVHhe7d0LXFRVHgfwHwzMIC8B5SmmqDOGouIj1PW12prrY9O1tcgUaysjV3y1ruKjTM1aH6lllq21kbusFJqvfIeBICgCIgIKishzBhhgGIZ5z9kzcNUrqwK2MJjn+/ncT95zLjhnZn73nP+9M2ZFKDAMU8+a+y/DMBQLBMPwsEAwDA8LBMPwsEAwDA8LBMPwsEAwDA8LBMPwsEAwDA8LBMPwsEAwDA8LBMPwsEAwDA8LBMPwsEAwDA8LBMPwsEAwDA8LBMPwsEAwDA8LBMPwsEAwDA8LBMPwsEAwDA8LBMPwsEAwDA8LBMPwsEAwDA8LBMPwPJmBIAQmgw46nR4GE9dm0kOnN8Boeoz/7WdiglGvpeMwwlg/DDpOo3lcRjzOw2pLT2QgTLXFSPsqBHOnzsDi3RnILc9DetQqvBa+B3svVXBHPX40hfE4um4Sgl9YiI2nylBRfBaHP/kbQtYfw4UyNXcU8zBP5gwhEMHRUwxfYzZuJO7EZwfjcTzbET7eHnB3tOUOevxYi5zh5uGLTlUxSIrZhW2Hr+JyuQckXd3gJGSr4+b4Vf3/IYxqKfLOn0VGQR2U9xuVc3d0DQjEWHFHWJn307dg856T2FfzPGa9NBvznnVuaG9n1OXXcO18ErLkgJ5ru4dHPwwI7INAbzu6o0LNyWVYFl2MHJc5WDLzeUwOtHQYpLh+PhmJVytxe4UK+KDX8BEYIbGnK7syXC8QwtXVGZ2cLftYf1WB0FScx5G1S7HrtAwFRq6Rz28ixr2+ADtm9IDAvF93BNtXnUOiIghrdk3D0zb1R7U7FZciEbl+LSIyCGq5tnsMCUXY/DmYP9yN7tQBt/Zi/tJbEA6eiFXLhsHcahHaChQWyVGb9QO+/vdhfJ9WARHXBfTDqJmv4o2X6UkoLwkHC5/D1HF9MbSnZWfoX1UgTAYVFCVFKK+hhSTXdg9hRzi5e6Kbq7BhX3UM218/hLPVgVh87C0Mp9PDI52fzEU6rVqtrK1gZfX/n2MMdZWoLC1BBS0D7p5heezd4eHZGR4O5pirYMj5DktmJUE/dhre+ftE9Go4qgUIrc/pRufL+jFxrS1Sl4Obh7Zh1t9/hkzujaDgEASHDEYPrts8a1yJokGPPI0skQsGL47G6hfFCOho4TnaHIgnk5KkHdpHPpo4mITOnU0+zSFEzfW0jJJU5seSPaG7ycGfckkZ12oxhlIS88l2snqsmLy9bhOJlnHtLXKTJHy+h+wOP0Qu6YxEx7U2m+wcObPx92TM064EvYPJm+sPk/O5Kq7zNiNRJG4iSweJCZynk5UJpURu4ros6MmrtHQlkMZ9jXeXb8Q/Ljmg54SB8Kk7gJ3LV2Dnz2WQ3ndqeRgd1FV5uBidhMzcivsvadqCMhMXoz5G2NIInNRKEDTBB5rkHdjw7k7sv2pC3X2nlgepxM2EFCT9mIkSI8H9Vp8PpM5GUtQ2rPn0DGIFU/CX997H2vApCOpFa4V7WMM5aDwmv/EyJvYfjWe8hXBuBwWchQNRjryYUzgSdw051XefdlIYj59+iEBExFGcSC29T4Gsh/r6KRzYaz4mAnv2HsTJxBsoo7+iyfWfSQtdVTGu5yrROVCMEcFhCPIfD4lVHhRKHXQteuOYWcHaRgQHN0d0sLNpqE0ehToHGTF768cT8e2/8Z998cgoUUHLdTfJUAtFaREKpEZInhuGYdPeQVDXp+Glu4VyVQvf1LCByMkBji4dIKRv0ua/TxUoPfYNPt0VjdiaoRizcDU2vCSB14PeZdaOEIp7IcDPA370mWsXZ2dupmhbeiVRSDNJwqEVZLanKxFI3iBLj5cTnUFDagsSSPzOEDJthIRIJC+RWVsSSIGR+znKoCghBXFR5Jt3xpFBA3rRY8Sku5cPCfjtIvLxpVpSY+AOfCATMRl0RKvVET03RZsMeqLTaunfT/samlqgkpRmRJIVkkVk6zfJ5BbX2nx1RHHzGknZvYi8OcmfiCUSIu7hS7xchpAZm0+RJFWTA2pgMhKj3jwuPV2MNDDv63R0nLShZeNKJ9+/vZIsGr2NnNYYiIZrfTg9Hcpx8unkPsQdItLt9+vJ3gLSxHIrn6SmnSDbtiYRqbSOa7Msy4RSkY7kyHV4dcEuHJBVwZgTg0sJaTiVHIOjX4Xjn4pn8cK6fdi3bwPWvtIfnrcfJclF/BfhmDv7Q2zPH4/5O77Dvv3RtDDuh07lJ/D1wVRIa5o6F9IiUWALodAWNtypz0pgA1uhELaCRykg6awgoGc3K2tYWwtaOEOoUX1jP3aEzMLMDYXQ/24jvtu3H1FfrcLcAYWIO30CPyZXc8c2wfz325jHZXPnTGvet7Wl46QNLRsXHYc1/X30dwpsBHSEzWBUwZiagJ/z81HuOgL+Eydhii/w8GtGPvD3H4mQVwPh3tl8ydjyLBMIBz9IxszB6nVb8I/PQjFNokVKxHKs3xqFFK8FmDbteUwdG4CAgB7w86TTav0P5SD2gzVYvesK8oPmIPyvryF45EAE9O2P4f194CaoQlFpFbSG+oPbkD0cOohga0XfjKIOdK+5NChPicSOeR/jM7kYI0PDsHDWFAQG9MXAkUPQvystCyrLIKu8752HVtYBInOYBELY0YQ3J+SmOiUyzx3HzdI6OPYdhJHD+sKhyRTawk5kD1cXEazpyag9aAeXXZMQMevPWBiZB/vJy7HtizV4sQvXdZtWgaJz4Vg2Ixpner6Fpf9ai8Vi7gmUH8fnYeuxI6MLxmzZgDWj/ODRoXVyrpNeRsqxL3HgkgnKO+9TLeoqC5FxQoYOgyTo0dsdjlxP/Xm51wRMnjwOk3vfbTXTFh5C9AfheH+XA576/HN8GXr7kmQVig9vwPyFp1D8hzCEh72MP/5PQfr/YoI04UscOX0ZqTKuqZ4ceXE3UFplh+5T+sGLvlnvhMLpKXT+zR+xYLwYne3vPs+6sovYt3QSVv5LAeHsrdi4aR6ed+c6HyOWmSHuIcGQZ/zQr1sAvP1GYlDjMNAyWafMRvzOaJw2DMaE+fOwyBwGWRIORn2LL97bgQO5XRDwQigWPtez1cJgZtIpUV2UhWtZmcjMvL1dxbUbRajQyiEtzkPOnXZuuylDeW3jaUuD4tiDOHToFpTj5+H9P5vDIENu4n5EfPwhNn9yASX+r+DNmZMxqdXC0EBXVYDC3EaPOfMGCqvKIVdJkZ+dhWx+39U85JapoGu0MjUY5VDIbaAxdYCLgxucnLiOx019JWFRalJ+ZAl50a8f6f3sNnJMVV+e3WVSkIr0rWRet07Eqnswee2fKeRK5mkSs30OCRrYh4h7TSPztyeQ69zhrYoWrgadhmg0/K2U3EqJIMvEYWTT7gSSe08f3XR6WtQ2Kml1aeTwkrFEbNWVeL76NTmWlE6unPmELJ89lPQUB5LBoz8i3xUom1nM/jLmCww6baPHrEkmkXOXk7CRm8kxhYoo7unTEi2t0k2NhqQuPUN2T/ckvnAgA9+KICeVXMdjxsIzBF13mC4hq9IJNroqOJXFIilNDyX/7KORoSYjDWdUdSBlP+HHtTPxwp/WYsXFAfjLtj344chnePe1oejJHd6qzEWmrQgiEX9zQUdnR9hZi2Bv74yO9/TRzdaGFrWN1scFl5FeWII8Ug7F8fUImz0D08MvQ/nMKkQeiMJ/vqXLja6OvI85tB7zBQZbYaPHLHKGo8iO1hH2cHS2h/M9fUIIaZXe+Ia8jdAbvt2FcBSqIJUWoljKdTyM+ePq7exz6RYNhL5ajezIWFR2kSBoViA608L51LksKOq4A8zM9w3kFZBbEXQfPwfzwldhRfgSLH07GDNGD0Lf3j5wqspHdkIsSk2m+3+0oVWpodZooScG6HQautcMdQpU0CWJsas/poR+gL+tXIkVS9/E3BenIKiPBOJuTpDFxSC3IB8q7kfalgZag/m7IjpotcZm3QsR0GXSoCFD4UbrhtKzFxDzc+7DH7shBefOxSM6XkFDwbW1A20bCHpG0OUcw96TsYhOzIIp7wRiKyRw9B+FieN6wM2OFpQFN1AryMfFr47gaFQGyoVesJf0RICaFrKKLpD8YRZCZk/F9OHe6AADCn/cgk1bd2N/vqiFlzwtyLsnenR0gpOcQN/ld5g9JwRzpgehvyftkyXg6MbF2HzqJvJUdu2hyGsWKzqruI9egNDg4eitPo7vt7yH1dvP4TrXf5cexcffw7o1XyIyVQknZ5tHuNTdegRrKO7PbcAIVdxHWLF9D745fQsOjgSiUSEY+JQbetak4fLFBJy4rIJBJUfBBTlMzl7oNaI33Fxt4Xj9GuJOJyO9SAaT8hYy09ORnnoByfFnUODshx6jZ2C0jyXudqpRU5qNuN15EI0egL6DfeHC9TyQvRMcjNUov5iGU3FpKDNVoyznCtLTs3A+7gwybhaBDJqBEYFi+LZuTf0AJbj0fSquF4ogef036E6XSE3fi6BHOHfDADq7OTiVoCAlCT9EpUIqUqMyL7vh9TJvF2KRTF/n+DIx+o+ZjJCRndF4RWlJbRsIOnCDPBd5F+NxtcgOxX1ewTsTesCPvuhWdlYwVhcjLvEq8tLdMWJZCF4O7g8v+mwJ7X3QZ4grDMWZSL0Qj/gEup09i7PnauETHI7QsD9hvI+NhZ5YHTQ1ZbiZrIb7mH7o7e+Jpi+wOMIjoBu6u6qQHxeLxJRExMfH4+zZiyiyGYZJqz/C3FG+6OrwiJ80/cUUKEqVQWXljqenD0AXAa2duJ4mde6LgWOGYqCbHqXpqbh8ORlJdGz1rxfdzl8rRefpO7EibCqm+Lugndx+uKPN70OY1JWoqihHpUYE4uIDsbuw4UUnWmgUchS
答案:
6、单选题:
选项:
A:
B:
C:
D:
答案:
7、单选题:
选项:
A:
B:
C:
D:
答案:
第五章 单元测试
1、单选题:
选项:
A:
B:
C:
D:
答案:
2、单选题:
选项:
A:
B:
C:
D:
答案:
3、单选题:
选项:
A: -1
B: 2
C: 1
D: 0
答案:
4、单选题:
选项:
A:
B:
C:
D:
答案:
5、单选题:
选项:
A: -17/4
B:0
C: 17/4
D: 1
答案:
6、单选题:
选项:
A:
B:
C:
D:
答案:
7、单选题:
选项:
A:
B:
C:
D:
答案:
8、单选题:
选项:
A:
B:
C:
D:
答案:
9、单选题:
选项:
A:
B:
C:
D:
答案:
10、单选题:
选项:
A:
B:
C:
D:
答案:


请先 !